تفاوت انتگرال معین و انتگرال نامعین
انتگرال گیری دو معنی و مفهوم در حساب دیفرانسیل و انتگرال دارد ، هر دو تعریف از دیدگاه ریاضی صحیح و پذیرفته شده است .
تعریف اول :انتگرال گیری یعنی یافتن مساحت محدود به منحنی ها ،حجم اجسام مختلف ،طول منحنی ها ،مرکز جرم اجسام و کاربردهای دیگر است . اگر دقت کنید این تعریف بیشتر به جنبه های کاربردی و مهندسی اشاره می کند .
مثلا در شکل بالا ما با داشتن معادله تابع (f(x و انتگرال گیری از ان تابع می توانیم مساحت محدود زیر این منحنی و محور x ها را بدست آوریم ، البته روش کار و قانون آن مفصل است که ما در بخشهای دیگر به آن می پردازیم .
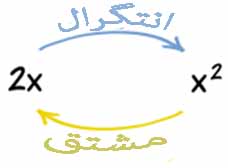
تعریف دوم :انتگرال گیری یعنی یافتن تابعی که مشتق آن معلوم باشد. در واقع ما با انتگرال گیری از تابع می توانیم اصل تابع را قبل از عمل مشتق گیری را بدست آوریم .یعنی انتگرال و مشتق دو عمل معکوس هم هستند.
مثلا در بالا نگاه کنید که چگونه مشتق و انتگرال معکوس هم هستند البته فعلا نگران نباشد چون گام به گام روشهای انتگرال گیری را با هم فرا می گیریم .خوب ما می دانیم که اگر از x به توان 2 مشتق بگیریم نتجه مشتق ما برابر با 2x است . اما اگر خود عبارت 2x را داشته باشیم چگونه می توان به تابعی رسید که اگر از آن مشتق بگیریم حاصل عبارت ما برابر با 2x می شود. جواب ساده است با کمک انتگرال گیری .
نماد انتگرال :
نماد انتگرال را با علامتی شبیه به حرف S نمایش می دهند که نشان دهنده علامت جمع است . مخففی از کلمه Sum یعنی جمع است .
در عبارت بالا ما از تابع 2x نسبت به متغیر x انتگرال می گیریم . که جواب آن بصورت زیر خواهد بود.
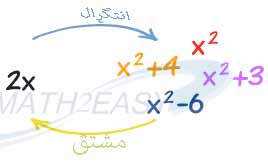
اینجا C یک مقدار ثابت است که به ثابت انتگرال معروف است .چرا این عدد C را باید بنویسیم دلیل آن خیلی ساده است ، ببینید اگر چه ما می دانیم که حاصل انتگرال فوق X به توان 2 است اما اصل تابع 2x ممکن است یکی از حالتهای زیر باشد .
به شکل بالا خوب دقت کنید هر کدام از عبارتهای سمت راست را اگر از آنها مشتق بگیریم حاصل همه آنها بعد از مشتق همان عبارت 2x خواهد بود به همین خاطر ما وقتی از 2x انتگرال گرفتیم حاصل جواب به اضافه عدد ثابت C می باشد .
پس آنچه در این پست فرا گرفتیم مفهوم اولیه انتگرال است ،و ارتباط انتگرال با عمل مشتق گیری همچنین کاربردهای آتی انتگرال در محاسبه حجم و مساحتها می باشد ، به عنوان آخرین مطلب این پست مفهوم انتگرال معین و نامعین را هم بطور مختصر بیان می کنیم .
انتگرال معین و نامعین:
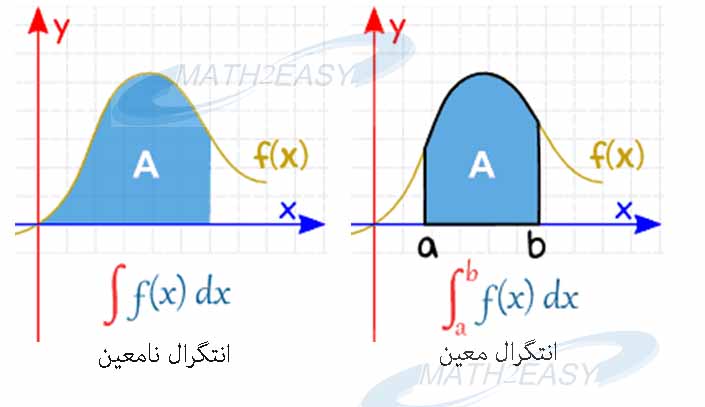
این دو نتگرال تنها در بازه انتگرال گیری با هم تفاوت دارند ، یعنی ما در هر دو حالت عمل انتگرال را ابتدا محاسبه می کنیم ،اما در انتگرال معین پس از بدست آمدن جاصل باید آن را در بازه مشخص اعمال کنیم شکل زیر فرق دو انتگرال را به سادگی نمایش می دهد.به تعبیری دیگر در انتگرال نامعین بازه انتگرال گیری مشخص نیست و فقط هدف ما عمل انتگرال است ،اما در انتگرال معین ما از همان ابتدا بازه انتگرال گیری مشخصی داریم و عمل انتگرال تابع در آن بازه محاسبه می شود.
- ۹۳/۰۸/۲۰
- ۱۲۴۰۷ نمایش


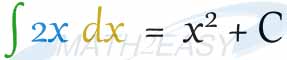


http://hegzaco.com